|
Science Frontiers ONLINE No. 127: Jan-Feb 2000 |
|
|
Some Magic Squares Are More Magical Than Others
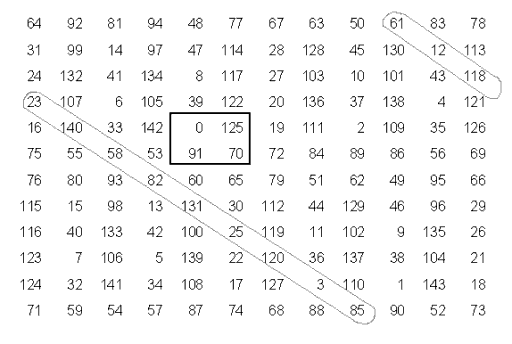
It is rather suprising that magic squares exist at all. Why should we be able to arrange 0 and the first 143 integers into a 12 x 12 square such that all columns, rows, and diagonals add up to 858? Believe it or not, there are actually more than two billion 12 x 12 magic squares! However, the particular 12 x 12 square reproduced here is more magical than most.
First off, it is "pandiagonal." This means that broken diagonals, such as those like 61-12-118 + 85-3-120-25-131 82-58-140-23 also add up to 858.
Second, this square is classified as "most-perfect" because the numbers in each and every 2 x 2 square add up to 286. How could a magic square be more perfect than this?
(Stewart, Ian; "Most-Perfect Magic Squares," Scientific American, 281:122, November 1999.)
Comment. We ask, with tongue-in-cheek: "Aren't we lucky to have such an interesting number system?"