Science Frontiers ONLINE No. 103: Jan-Feb 1996 Issue Contents

Other pages Home Page Science Frontiers Online All Issues This Issue Sourcebook Project Sourcebook Subjects

How To Find A Piece Of Pi

The formula shown below allows one -- if one wishes -- to find the billionth digit of pi without first computing the preceding 999,999,999 digits. In other words, isolated digits of pi can be quickly calculated should an urgent need arise. P.B. Borwein et al, at Simon Fraser University, announced this "curious" discovery in October 1995.

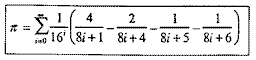This is the equation mathematicians use in calculating isolated digits of pi.

Innuendo aside, there is something more than "curious" here. It seems that the formula works only for hexadecimal (base-16) digits of pi. These can be easily converted into binary (base-2) digits. Strangely, it does not work at all for our familiar decimal (base-10) digits of pi.

Not to worry though! Y. Kanada and colleagues, at the University of Tokyo, have now computed pi to 4,294,960,000 decimal digits. But, they have found a puzzling asymmetry. In the first 4 billion digits, the decimal digit 6 occurs 400,033,035 times, but 2 shows up only 399,965,405 times! Shouldn't all ten digits appear with the same frequency? Obviously, we do not appreciate all of the subtleties of pi.

(Peterson, I.; "A New Formula for Picking Off Pieces of Pi," Science News, 148:279, 1995.)

From Science Frontiers #103, JAN-FEB 1996. � 1996-2000 William R. Corliss

---